State of the Art(ificial): Part 1

Understanding rigid contact lens design & fitting

Artificial intelligence (AI) is getting a lot of attention lately, almost to the point of becoming a fashion statement: everybody is into artificial intelligence, it seems. A recent article by Hood et al in Optometry & Vision Science – one of our leading journals in the profession –shows that big data and AI will become important within the field of eyecare too. This article looked at using optical coherence tomography (OCT) images of the retina to create a reference database for glaucoma detection. In short, if you create databases with images of thousands of healthy eyes, it is not too difficult to see what is normal and what is not. The same has been successfully applied to detect diabetic retinopathy and ocular hypertension. It seems that (objective) technology can be better than (subjective) human beings at detecting anomalies.

How about our contact lens industry? Guess what: we are very much underway in the same direction, maybe without always realising it. Look at myopia management (comparing a myopic kid’s eyes to a database of age-matched controls) or at keratoconus detection (the indices marked in ‘red’ or ‘green’ on the corneal topography map indicate whether a cornea is abnormal or not). But it’s not just in detection; in fitting contact lenses, large databases can also be used to predict outcomes. Maybe not always to allow ‘self-learning’ yet – but that would be the logical next step. Let’s see where we are right now in our industry: a state of the art(ificial) with regard to contact lens fitting. In this first part (of two), we focus on rigid corneal lenses and ortho-k.

Metrics

First off: the metric system is gaining territory in optics & optometry. This is happening now too in myopia management, arguably the hottest topic of the moment. Eye measurements for myopia management are expressed in millimeters of axial length, which is supposedly a much more important parameter than dioptric values and refractive error. For example, the normal eye is defined as 23.5 mm, whereas the abnormal eye is ‘simply’ expressed as any eye over 26.0 mm of axial length, with increased risk of myopic retinopathy. Progression of myopia is measured in 0,1 mm steps (for some age groups, 0,1 mm is considered ‘normal’ progression). However, it may be better to express these measurements in microns if they are less than 0,1 mm. Changes in axial length, for instance, of 50 microns or 80 microns, etc, resonate better (especially with parents) compared to 0,05 mm or 0,08 mm. This is certainly the case with corneal, ortho-k and scleral lens parameters, as the differences can be even smaller and more subtle. Contact lens trial sets increasingly use elevation data in microns (as opposed to millimeters of curvature), certainly in the soft and scleral lens arena.

So, what is a micron again? Most of us in Europe are familiar with kilometres: the highest peak in Austria (the Großglockner), for instance, is 3,798 kilometres high, or 3798 meters. If an adult would take one standard ‘step’ while walking, this would represent 0,74 meters (as per standardization under Agrippa). So, four steps would be 3,048 meters. In the metric system, the ‘step’ from meter to millimetre is the same as from kilometre to meter (a step of 1/1000). A typical scleral lens may have a height of 3,776 millimetres – or 3776 micrometres (or microns), which is another 1/1000 step. For small increments, like many in our contact lens industry, this is absolutely the unit to use. To put things in perspective, for instance, the human tear film (without contact lens) is thought to be anywhere between 2-5 microns thick (which would be inconveniently 0,002-0,005 if put in millimetres). In comparison, the corneal epithelial layer is 50 microns thick, but subtle changes applied to the epithelium by ortho-k would be, for instance, between 0- to 20-micron. A soft lens on that ocular surface is typically invasive, by the way, and would be around 80-120 microns (compared to a small tear film of only 2-5 microns). The post-lens tear film in soft lens wear would be extremely small (maybe 1-2 microns). 

Workbench

To understand the use of large databases and corneal detection in contact lens fitting, let’s shift our attention to measuring the ocular surface using microns. Because here too, subtle differences in elevation in the ‘y-direction’ can be detected using the fantastic corneal topography technology that so many of us have within reach. If we plot a healthy cornea over an area of a 9 mm chord (4.5 mm from the centre, which would be roughly the area where a corneal rigid lens would land), then we see the following interesting results (Hickson-Curran et al, Optometry & Vision Science 2014): The elevation of the ‘standard eye’ is determined by taking the average (and distribution) of the base curve and eccentricity.

To define ‘a standard eye’ over a 9 mm, we can take the average value of 1445 microns, and then take one standard deviation on each side; this would represent the 68% of corneas that are most prominent in the normal population – in other words, the bulk of the eyes in a normal practice. 

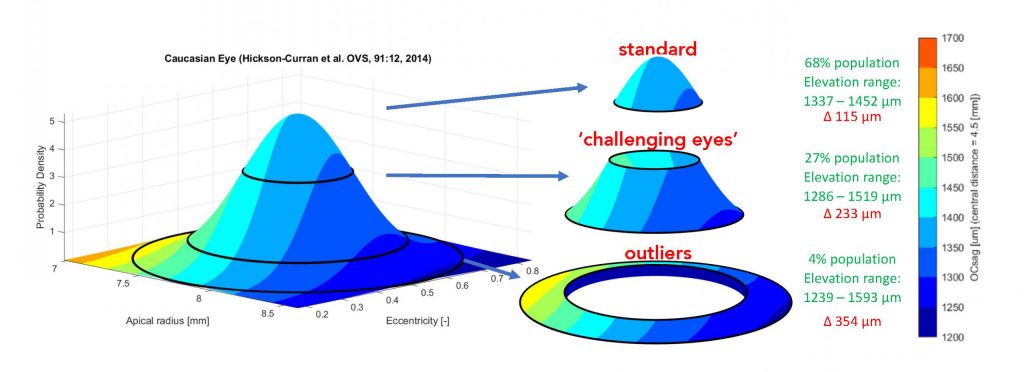
These eyes would range in sagittal height (OC-SAG) from 1337 and 1454 microns over the given chord (see figure 1). Hence, the difference is 115 microns: a narrow range, in fact. Calculations with a Menicon Genius rigid corneal lens design (a lens with a spherical optical zone and an aspherical periphery) indicated that a base curve of 7,55 mm to 8,10 mm would suffice to fit all of these eyes (68% of all eyes). Interestingly, for the next category, the following 27% of eyes (or two standard deviations) range from 1286–1519 microns – a difference of 233 microns. This would be equal to using base curves from 7,25 to 8,40 mm. Let’s call these the ‘out-of-standard’ eyes. The next category would be ‘the outliers’: three standard deviations and the remaining 4% of eyes in a normal population. Corneas in this category range from 1239–1593 microns, a 354-micron difference, in OC-SAG over the 9 mm chord, and for these eyes your trial set would need to include base curves from 7,00 to 8,70 mm.

Rigid Corneal Lenses & Ortho-k

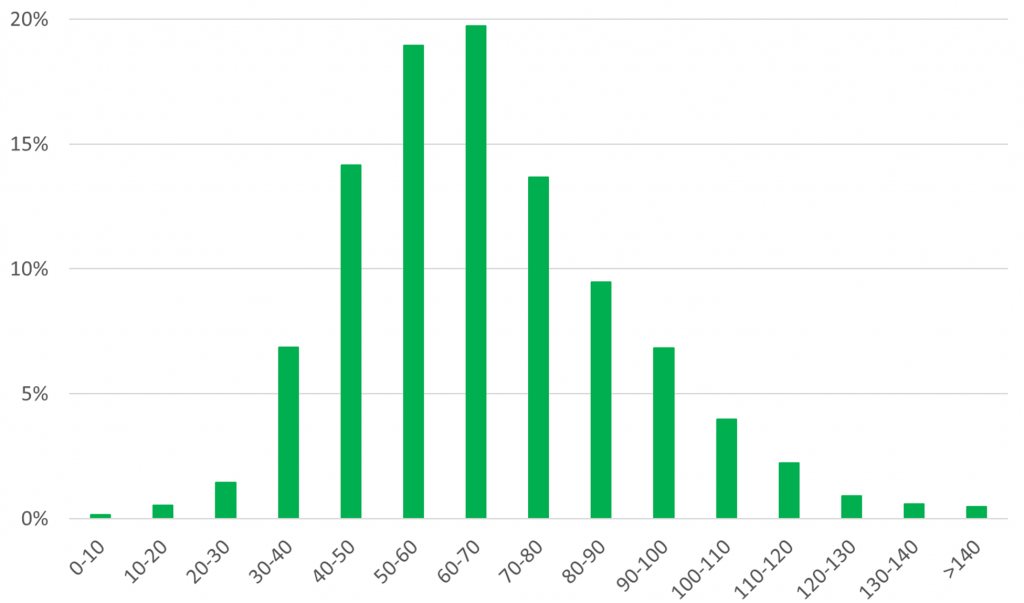
Next, what elevation difference on the ocular surface would justify a toric back-surface design rather than a standard (spherical or aspherical) back-surface design? Studies at Pacific University presented at the Global Specialty Lens Symposium have revealed that if there is more than 30 microns of elevation difference on the ocular surface, then some sort of back-surface adjustments should be required (e.g., toric or more complex shapes) for both corneal rigid lenses and orthokeratology (ortho-k) lenses. Work by Menicon in the Netherlands, based on a database of 125.000 ortho-k lenses, seems to support this data: the popularity of toric lens designs starts to become ‘mainstream’ pretty much at 30-40 microns of height difference between the flattest and the steepest meridian of ordered ortho-k lenses (see figure 2). 

Scleral Lenses

Next is to decide when to use a ‘scleral’ rather than a rigid corneal lens when the irregularities on the ocular surface are larger in scale. Another study at Pacific University by Randy Kojima et al. (2023) showed that 96% of eyes with 0-100 microns of elevation difference and 94% of eyes with 101-200 microns of elevation difference were successfully fit with corneal lenses. However, only roughly one in three eyes with an elevation differential between 201-400 microns could be fit in corneal lenses. They concluded that eyes with under 200 microns of elevation difference can confidently be fitted with corneal lenses, while eyes with over 400 microns of elevation difference may require scleral lenses due to the increased corneal irregularity.

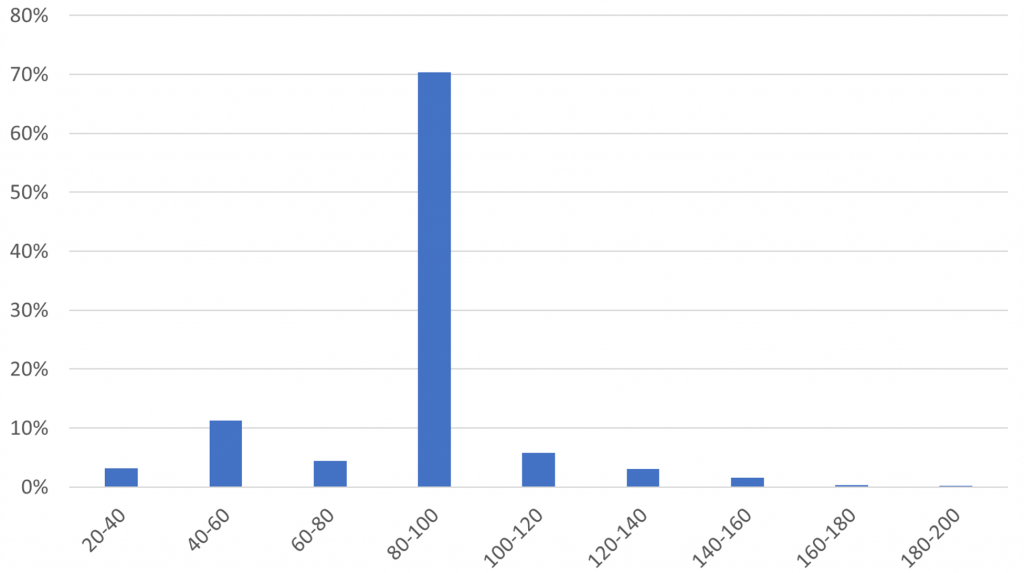
How about when to ‘go toric’ with scleral lenses? That is still a debate in our industry and within our profession. One would guess that for scleral lenses, the height differential values are much larger, as these differences can be greater on the scleral portion of the ocular surface. Based on historical data, this indeed has been suggested (DeNaeyer et al. 2017) to maybe be in the 300-micron range of elevation difference (on a 16-mm concentric circle around the apex). However, recent data presented at a Menicon inspiration event in Amersfoort in the Netherlands showed that 70% of ordered scleral lenses have relatively small height differences between the steepest and flattest meridian of only 80-100 microns (see figure 3). And some of the scleral lenses manufactured show height differences of only 40-60 microns. Interestingly, and maybe not surprising given the previous information, 97% of scleral lenses produced by this manufacturer are toric.

We are increasingly in control over the (scleral) lens fit. The scleral landing zone pressure can now be calculated quite precisely, including where the scleral lens lands in the periphery and how much pressure this would generate. For instance, a standard scleral lens with a standard peripheral shape (a landing zone angle in this example) would exert 100% pressure just outside the limbus. By changing the landing zone angle slightly, the pressure distribution is altered by small amounts, e.g., the peak in the pressure distribution of 105% would add eight microns of conjunctival compression (for a flat fit, see figure 4), and a peak of 115% would be an increase of 23 microns of conjunctival compression (for a steep fit). We can ‘play’ with this regarding scleral lens fit and therefore influence the amount of scleral blanching.

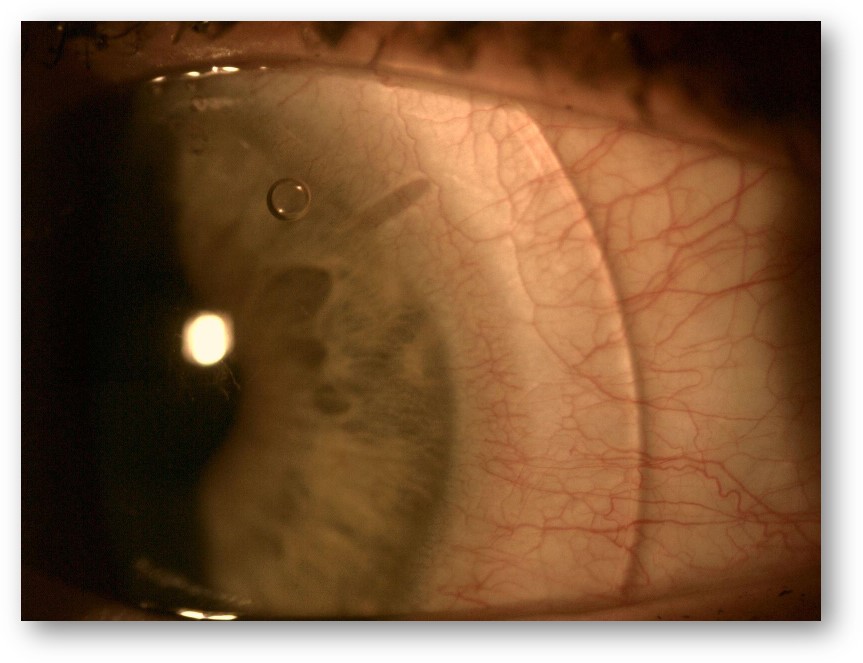
If you take into account that standard conjunctival capillaries are about 10-20 microns in diameter, and a human red blood cell is about eight microns in size – one can imagine that ‘increasing’ the pressure on the vessels by a little over ten microns may physically limit the circulation of red blood cells in the given capillaries, causing blanching of the area and showing a nice visualisation of the interaction between the lens and eye. 

Closing Remarks

In some parts of the world, and the Netherlands is one of them, topography-based fitting has become the standard for rigid lenses. Most corneal lens fits are topography-based. This means that either eye care practitioners use corneal topography with applied software to design a lens themselves, or (more commonly) they upload the topography to the manufacturer and ‘the perfect’ lens is designed – again using thousands of corneas in their databases as references. This is certainly the case for ortho-k lens fits: almost all ortho-k lenses in the Netherlands are ‘topography-based’, and trial-sets are hardly used. Scleral lenses, assuming that correct anterior ocular surface shape data is available over a sufficient area, could go the same route. 

In the next part of this two-part article, we shall focus on what all this means in terms of soft lens fitting. Can we use the base-database there too? Is there room for custom-made soft lenses? Or is the soft lens modality moving more into a ‘one-size-fits-all’ direction? And what are the soft lens options for the irregular cornea?

Acknowledgements

Special thanks to Randy Kojima for his contributions to elevation data usage in this article.

References

1 Hood DC, Durbin M, Lee C, Gomide G, La Bruna S, Chaglasian M, Tsamis E. Toward a Real-world Optical Coherence Tomography Reference Database: Optometric Practices as a Source of Healthy Eyes. Optom Vis Sci. 2023 Aug 1;100(8):499-506. doi: 10.1097/OPX.0000000000002049. Epub 2023 Jul 27. PMID: 37499165.
2 Hickson-Curran et al. Comparative evaluation of Asian and white ocular topography. Optom Vis Sci. 2014 Dec;91(12):1396-405. doi: 10.1097/OPX.0000000000000413. PMID: 25325762.
3 Turpin et al. When is a Toric Orthokeratology Lens Design Indicated? Poster Global Specialty Lens Symposium 2018, Las Vegas (USA).
4 Kojima et al. How Often Should We Prescribe Toric Orthokeratology Lenses? Poster Global Specialty Lens Symposium 2021, Las Vegas (USA).
5 Kojima et al. To Corneal GP or not to Corneal GP, that is the Question? Poster Global Specialty Lens Symposium 2023, Las Vegas (USA).
6 DeNaeyer et al. Qualitative Assessment of Scleral Shape Patterns Using a New Wide Field Ocular Surface Elevation Topographer – The SSSG Study.Journal of Contact Lens Research and Science. Nov 2017. https://doi.org/10.22374/jclrs.v1i1.11.